I°) La méthode Monte Carlo, c’est quoi ?!
Le terme méthode de Monte-Carlo, ou méthode Monte-Carlo, désigne une famille de méthodes algorithmiques visant à calculer une valeur numérique approchée en utilisant des procédés aléatoires, c’est-à-dire des techniques probabilistes. Le nom de ces méthodes, qui fait allusion aux jeux de hasard pratiqués à Monte-Carlo, a été inventé en 1947 par Nicholas Metropolis, et publié pour la première fois en 1949 dans un article coécrit avec Stanislaw Ulam.
Cf Wikipedia.
II°) Mmh… Concrétement ?!
Pour approximer PI avec cette méthode, il faut jouer au lancer de fléchettes. Le cadre est un cercle inscrit dans un carré.
1- Cible vide 2- Cible entrain de se remplir 3- Cible pleine
La fléchette peut atteindre le carré ou le cercle. En comptant le nombre de fléchettes atteignant le cercle, par rapport au nombre total de fléchettes lancés, nous pouvons approximer PI.
En effet, l’aire d’un cercle de rayon R est : π*R², et l’aire du carré est 4*R² dans ce cas là et si l’on s’intéresse au Ratio du nombre de fléchettes ayant touché le cercle par rapport à au nombre total, nous pouvons en dégager π , à condition que le nombre de lancer soit suffisamment grand.
Ratio = Aire cercle / Aire carré
= π*R² / 4*R²
= π / 4
π = 4 * Ratio
Cette méthode repose sur le fait que la loi de probabilité de tirage est uniforme.
III°) Pseudo code
- 1- : Afficher le cadre (Carré et cercle).
- 2- : Pour chaque fléchette, l’envoyer de façon aléatoire sur la cible.
- 2-1 : Vérifier si la fléchette est dans le cercle, compter.
- 2-2 : L’afficher, calculer l’approximation et récupérer le meilleur score.
- 2-3 : Répéter étape 2-.
IV°) Code
// *****************************************************************************
// PARAMETERS
// *****************************************************************************
float r = 480; // Radius
int total = 0; // Cnt
int circle = 0; // Cnt
int nbrDarts = 10000; // Nbr of Darts by frame
double record_PI; // Get the best approx
int correctDigit; // Get the correct number of digit
// *****************************************************************************
// SETUP
// *****************************************************************************
void setup() {
size(960, 960);
surface.setLocation(0, 0);
background(0);
translate(width/2, height/2);
stroke(0, 0, 255);
strokeWeight(3);
noFill();
ellipse(0, 0, 2*r-4, 2*r-4);
rectMode(CENTER);
rect(0, 0, 2*r-4, 2*r-4);
record_PI = 0;
}
// *****************************************************************************
// DRAW
// *****************************************************************************
void draw() {
translate(width/2, height/2);
double pi = 0;
strokeWeight(0.5);
// Throw 10 000 darts at the time
for (int i = 0; i < nbrDarts; i++) {
// Create the dart
double x = random(-r, r);
double y = random(-r, r);
// Check if it is inside the circle area, or not
double d = (double)(x*x + y*y);
if (d < (double)r*(double)r) {
stroke(0, 255, 0, 100); // Inside the circle
circle++;
} else {
stroke(255, 0, 0, 100);
}
total++;
// Display it
point((float)x, (float)y);
// Calculate the approximation of pi
pi = (double)4 * ((double)circle / (double)total);
// Getting the best record and displaying it on the console
double recordDiff = Math.abs(Math.PI - record_PI);
double diff = Math.abs(Math.PI - pi);
if (diff < recordDiff) {
recordDiff = diff;
record_PI = pi;
correctDigit = findDifference(Math.PI, pi); // Get the correct digit number of the approximation of PI
if (correctDigit < 0) correctDigit = 0;
println(record_PI + " , nbr good digits = " + correctDigit);
}
}
}
// *****************************************************************************
// METHODS
// *****************************************************************************
// ******************************************
int findDifference(double a, double b) {
Character ch = Character.MIN_VALUE;
String a_s = Double.toString(a).replace('.', ch);
String b_s = Double.toString(b).replace('.', ch);
for (int i = 0; i < Math.min(a_s.length(), b_s.length()); i++) {
if (a_s.charAt(i) != b_s.charAt(i)) return i-1;
}
return 0;
}
V°) Résultats
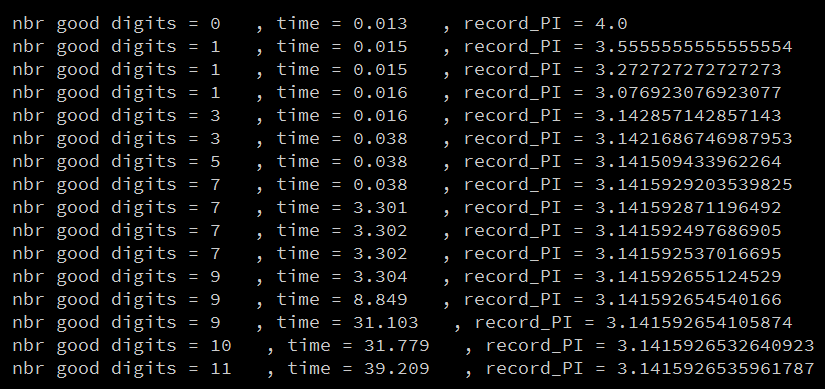
Dans cette simulation, j’utilise 10 000 fléchettes par frame d’animation. Ayant un taux de FPS de 60, j’ai donc 10 000 * 60 = 600 000 fléchettes lancés par secondes. Le nombre de digits correct augmente rapidement avant de se stabiliser à 11, qui représente ma limite. J’utilise en effet des variables de type double.
J’obtiens :