Dans ce post, nous allons nous intéresser à simuler et visualiser un pendule double.
Le pendule double consiste en un pendule à l’extrémité duquel on accroche un autre pendule. C’est un exercice classique de mécanique. On a donc deux tiges de longueur l1 et l2, de masse nulle ainsi que de deux masses m1 et m2. Son évolution est généralement chaotique.
I°) Les equations de mouvement
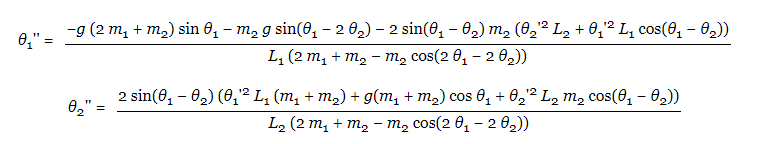
Ces equations proviennent des equations cinématiques, et des forces du pendule double. Pour plus d’informations sur la manière de les obtenir, allez sur ce site :
https://www.myphysicslab.com/pendulum/double-pendulum-en.html.
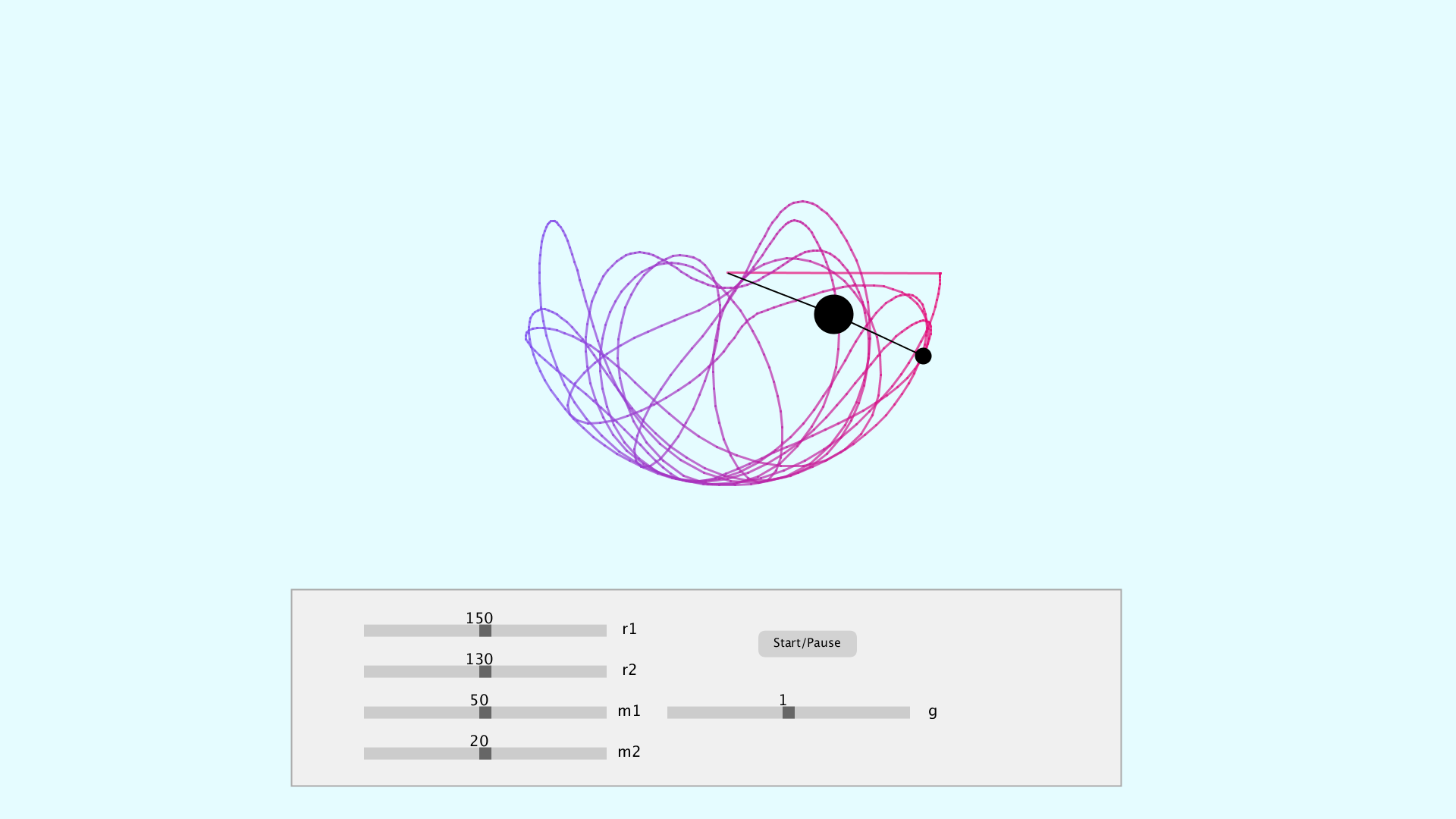
II°) Résultats
III°) Code
Ce code est composé en deux parties :
- La simulation et visualisation du pendule double,
- La création d’une interface utilisateur interactive.
III-1°) Simulation et visualisation
Le double pendule nécessite un bon paquet d’informations, notamment la longueur des axes : r1 et r2, la masses des pendules : m1 et m2, l’angle des pendules : a1 et a2, leurs vitesses a1_v et a2_v ainsi que leurs acceleration a1_a et a2_a.
// *****************************************************************************
// PARAMETERS
// *****************************************************************************
// Double pendulum parameters
float r1 = 150; // Radius axe n°1
float r2 = 130; // Radius axe n°2
float m1 = 50; // Masse object n°1
float m2 = 20; // Masse object n°2
float a1 = PI/2; // Angle n°1
float a2 = PI/2; // Angle n°2
float a1_v = 0; // Velocity n°1
float a2_v = 0; // Velocity n°2
float a1_a = 0; // Acceleration n°1
float a2_a = 0; // Acceleration n°2
float g = 0.1; // gravitational acceleration
D’autres paramètres liés à l’affichage du pendule double, et particulièrement à sa trace sont nécessaires :
// Ghost parameters
float px2 = -1;
float py2 = -1;
PGraphics canvas;
int cnt = 0;
color[] colours = new color[4];
// Translation parameters
float cx;
float cy;
Enfin, des paramètres pour convertir les coordonnées polaires en cartésiennes sont nécessaires.
// Cartesian position
float x1, x2, y1, y2;
Dans la partie setup(), nous retrouvons : l’initialisation des couleurs que l’on souhaite utiliser, de la trace du pendule double et enfin le calcul des coordonnées cartésiennes des deux pendules.
// *****************************************************************************
// SETUP
// *****************************************************************************
void setup() {
fullScreen();
//size(900, 900);
// Init colors
colorMode(RGB, 255, 255, 255, 1);
pixelDensity(1);
colours[0] = color(229, 252, 255, 0.3);
colours[1] = color(122, 79, 242, 0.7);
colours[2] = color(230, 9, 116, 0.7);
colours[3] = color(229, 252, 255);
// Init ghost
cx = width/2;
cy = height/3;
canvas = createGraphics(width, height);
canvas.beginDraw();
canvas.background(colours[3]);
canvas.endDraw();
// Let's do the calculation at least once
x1 = r1 * sin(a1);
y1 = r1 * cos(a1);
x2 = x1 + r2 * sin(a2);
y2 = y1 + r2 * cos(a2);
}
Enfin, dans la partie draw(), nous avons :
// *****************************************************************************
// DRAW
// *****************************************************************************
void draw() {
image(canvas, 0, 0);
stroke(170);
fill(240);
rect(width/5, 0.72*height, 0.57*width, 0.24*height);
noStroke();
noFill();
// Display pendulum
stroke(0);
strokeWeight(2);
translate(cx, cy);
line(0, 0, x1, y1);
fill(0);
ellipse(x1, y1, m1, m1);
line(x1, y1, x2, y2);
fill(0);
ellipse(x2, y2, m2, m2);
// Motion equations
float num1 = -g*(2*m1 + m2) * sin(a1) - m2*g*sin(a1-2*a2) -2*sin(a1 - a2)*m2*(a2_v*a2_v*r2 + a1_v*a1_v*r1*cos(a1-a2));
float den1 = r1*(2 * m1 + m2 - m2 * cos(2*a1 - 2*a2));
a1_a = num1/den1;
float num2 = 2*sin(a1-a2)*(a1_v*a1_v*r1*(m1+m2) + g*(m1+m2)*cos(a1) + a2_v*a2_v*r2*m2*cos(a1-a2));
float den2 = r2*(2*m1 + m2 - m2*cos(2*a1 - 2*a2));
a2_a = num2/den2;
// Calculate cartesian coordinates
x1 = r1 * sin(a1);
y1 = r1 * cos(a1);
x2 = x1 + r2 * sin(a2);
y2 = y1 + r2 * cos(a2);
// Get velocity and acceleration
a1_v += a1_a;
a2_v += a2_a;
a1 += a1_v;
a2 += a2_v;
// Let's add a damping factor
a1_v *= 0.999;
a2_v *= 0.999;
// Displaying the ghost of the double pendulum
canvas.beginDraw();
canvas.translate(cx, cy);
canvas.strokeWeight(3);
if (frameCount > 1) {
// Let's put a color gradient effect between purple and red colors.
float trans = map(x2, -1*(r1+r2), r1 + r2, 0, 1);
color lineColour = lerpColor(colours[1], colours[2], trans);
canvas.stroke(lineColour);
canvas.line(px2, py2, x2, y2);
}
canvas.endDraw();
px2 = x2;
py2 = y2;
}
III-2°) Interface utilisateur (GUI)
Dans cette partie, j’utilise des classes pour créer mon bouton Play/Pause, ainsi que les HScrollbar. Je les instancie dans la partie maître, et check en permanent leur état afin de rendre cette interface interactive.
La classe Button pour le bouton Play/Pause est la suivante :
class Button {
// *****************************************************************************
// PARAMETERS
// *****************************************************************************
float xpos; // X pos of the button
float ypos;
float widthButton;
float heightButton;
color rectColor;
color rectHighlight;
boolean rectOver = false;
boolean locked = false;
int cnt = 0;
String name;
boolean state = false;
// *****************************************************************************
// CONSTRUCTOR
// *****************************************************************************
Button(float xpos_, float ypos_, float widthButton_, float heightButton_, String name_) {
xpos = xpos_;
ypos = ypos_;
widthButton = widthButton_;
heightButton = heightButton_;
name = name_;
rectColor = color(210);
rectHighlight = color(190);
}
// *****************************************************************************
// METHODS
// *****************************************************************************
// ***********************
boolean overRect(float x, float y, float width, float height) {
if (mouseX >= x && mouseX <= x+width &&
mouseY >= y && mouseY <= y+height) {
return true;
} else {
return false;
}
}
// ***********************
boolean update() {
if (overRect(xpos, ypos, widthButton, heightButton)) {
rectOver = true;
if (mousePressed == true && locked == false) {
locked = true;
state = !state;
delay(200);
locked = false;
}
} else {
rectOver = false;
}
return state;
}
// ***********************
void display() {
noStroke();
if (rectOver) {
fill(rectHighlight);
} else {
fill(rectColor);
}
rect(xpos, ypos, widthButton, heightButton, 10, 10, 10, 10);
textSize(16);
textAlign(CENTER, CENTER);
fill(0);
text(name, xpos, ypos-4, widthButton, heightButton);
textAlign(CENTER);
}
}
La classe Hscrollbar pour les sliders est la suivante :
class HScrollbar {
// *****************************************************************************
// PARAMETERS
// *****************************************************************************
int swidth, sheight; // width and height of bar
float xpos, ypos; // x and y position of bar
float spos, newspos; // x position of slider
float sposMin, sposMax; // max and min values of slider
int loose; // how loose/heavy
boolean over; // is the mouse over the slider?
boolean locked;
float ratio;
String name;
int sh, sw;
float min, max;
float spos_map;
// *****************************************************************************
// CONSTRUCTOR
// *****************************************************************************
HScrollbar (float xp, float yp, int sw_, int sh_, int l, String name_, float min_, float max_, float beginValue_) {
swidth = sw_;
sheight = sh_;
int widthtoheight = sw_ - sh_;
ratio = (float)sw_ / (float)widthtoheight;
xpos = xp;
ypos = yp-sheight/2;
spos = xpos + swidth/2 - sheight/2;
newspos = spos;
sposMin = xpos;
sposMax = xpos + swidth - sheight;
loose = l;
name = name_;
min = min_;
max = max_;
spos_map = beginValue_;
}
// *****************************************************************************
// METHODS
// *****************************************************************************
// ***********************
void update() {
if (overEvent()) {
over = true;
} else {
over = false;
}
if (mousePressed && over) {
locked = true;
}
if (!mousePressed) {
locked = false;
}
if (locked) {
newspos = constrain(mouseX-sheight/2, xpos, xpos + swidth - sheight);
}
if (abs(newspos - spos) > 1) {
spos = spos + (newspos-spos)/loose;
spos_map = map(spos, xpos, xpos + swidth - 1.5*sheight, min, max);
}
}
// ***********************
float constrain(float val, float minv, float maxv) {
return min(max(val, minv), maxv);
}
// ***********************
boolean overEvent() {
if (mouseX > xpos && mouseX < xpos+swidth &&
mouseY > ypos && mouseY < ypos+sheight) {
return true;
} else {
return false;
}
}
// ***********************
void display() {
noStroke();
fill(204);
rect(xpos, ypos, swidth, sheight);
textSize(20);
textAlign(CENTER);
fill(0);
text(name, xpos + swidth + 30, ypos + 0.8*sheight );
text((int)spos_map, spos, ypos-2);
if (over || locked) {
fill(0, 0, 0);
} else {
fill(102, 102, 102);
}
rect(spos, ypos, sheight, sheight);
}
// ***********************
float getPos() {
return (float)spos_map;
//return (float)spos_map * ratio;
}
}
Enfin, la classe maître devient :
// *****************************************************************************
// PARAMETERS
// *****************************************************************************
// Double pendulum parameters
float r1 = 150; // Radius axe n°1
float r2 = 130; // Radius axe n°2
float m1 = 50; // Masse object n°1
float m2 = 20; // Masse object n°2
float a1 = PI/2; // Angle n°1
float a2 = PI/2; // Angle n°2
float a1_v = 0; // Velocity n°1
float a2_v = 0; // Velocity n°2
float a1_a = 0; // Acceleration n°1
float a2_a = 0; // Acceleration n°2
float g = 0.1; // gravitational acceleration
// Translation parameters
float cx;
float cy;
// Ghost parameters
float px2 = -1;
float py2 = -1;
PGraphics canvas;
int cnt = 0;
color[] colours = new color[4];
// Cartesian position
float x1, x2, y1, y2;
// GUI Parameters
HScrollbar hs_r1, hs_r2, hs_m1, hs_m2, hs_a1, hs_a2, hs_g;
Button b_start, b_stop, b_reset;
// *****************************************************************************
// SETUP
// *****************************************************************************
void setup() {
fullScreen();
//size(900, 900);
// Init colors
colorMode(RGB, 255, 255, 255, 1);
pixelDensity(1);
colours[0] = color(229, 252, 255, 0.3);
colours[1] = color(122, 79, 242, 0.7);
colours[2] = color(230, 9, 116, 0.7);
colours[3] = color(229, 252, 255);
// Init ghost
cx = width/2;
cy = height/3;
canvas = createGraphics(width, height);
canvas.beginDraw();
canvas.background(colours[3]);
canvas.endDraw();
// Let's do the calculation at least once
x1 = r1 * sin(a1);
y1 = r1 * cos(a1);
x2 = x1 + r2 * sin(a2);
y2 = y1 + r2 * cos(a2);
hs_r1 = new HScrollbar(width/4, 0.77*height, width/6, 16, 1, "r1", 10, 200, 150);
hs_r2 = new HScrollbar(width/4, 0.82*height, width/6, 16, 1, "r2", 10, 200, 130);
hs_m1 = new HScrollbar(width/4, 0.87*height, width/6, 16, 1, "m1", 10, 100, 50);
hs_m2 = new HScrollbar(width/4, 0.92*height, width/6, 16, 1, "m2", 10, 100, 20);
hs_g = new HScrollbar(width/4 + 80 + width/6, 0.87*height, width/6, 16, 1, "g", 0, 20, 1);
b_start = new Button(width/3 + 40 + width/6, 0.77*height, 130, 35, "Start/Pause");
}
// *****************************************************************************
// DRAW
// *****************************************************************************
void draw() {
image(canvas, 0, 0);
stroke(170);
fill(240);
rect(width/5, 0.72*height, 0.57*width, 0.24*height);
noStroke();
noFill();
// Get all GUI parameters
hs_r1.update();
hs_r1.display();
hs_r2.update();
hs_r2.display();
hs_m1.update();
hs_m1.display();
hs_m2.update();
hs_m2.display();
hs_g.update();
hs_g.display();
// And use them here...
boolean start = b_start.update();
b_start.display();
r1 = hs_r1.getPos();
r2 = hs_r2.getPos();
m1 = hs_m1.getPos();
m2 = hs_m2.getPos();
g = hs_g.getPos();
// Display pendulum
stroke(0);
strokeWeight(2);
translate(cx, cy);
line(0, 0, x1, y1);
fill(0);
ellipse(x1, y1, m1, m1);
line(x1, y1, x2, y2);
fill(0);
ellipse(x2, y2, m2, m2);
if (start) {
// Motion equations
float num1 = -g*(2*m1 + m2) * sin(a1) - m2*g*sin(a1-2*a2) -2*sin(a1 - a2)*m2*(a2_v*a2_v*r2 + a1_v*a1_v*r1*cos(a1-a2));
float den1 = r1*(2 * m1 + m2 - m2 * cos(2*a1 - 2*a2));
a1_a = num1/den1;
float num2 = 2*sin(a1-a2)*(a1_v*a1_v*r1*(m1+m2) + g*(m1+m2)*cos(a1) + a2_v*a2_v*r2*m2*cos(a1-a2));
float den2 = r2*(2*m1 + m2 - m2*cos(2*a1 - 2*a2));
a2_a = num2/den2;
// Calculate cartesian coordinates
x1 = r1 * sin(a1);
y1 = r1 * cos(a1);
x2 = x1 + r2 * sin(a2);
y2 = y1 + r2 * cos(a2);
// Get velocity and acceleration
a1_v += a1_a;
a2_v += a2_a;
a1 += a1_v;
a2 += a2_v;
// Let's add a damping factor
a1_v *= 0.999;
a2_v *= 0.999;
// Displaying the ghost of the double pendulum
canvas.beginDraw();
canvas.translate(cx, cy);
canvas.strokeWeight(3);
if (frameCount > 1) {
// Let's put a color gradient effect between purple and red colors.
float trans = map(x2, -1*(r1+r2), r1 + r2, 0, 1);
color lineColour = lerpColor(colours[1], colours[2], trans);
canvas.stroke(lineColour);
canvas.line(px2, py2, x2, y2);
}
canvas.endDraw();
px2 = x2;
py2 = y2;
}
}
